Now suppose A and B be two subsets of the set of integers. Then some
elements of A may be related to some elements of B by a relation, say, 'x is less than y' where
x ЄA and y Є B.
Now if we construct a set consisting of ordered pairs of the type (x, y) where x
ЄA and y Є B and also x < y then the set so formed is called 'a relation form A to B'.
Normally a relation is denoted by R. Here x Є A is associated to y Є B by the relation 'x is less than y' and we denote it as xRy.
Related Questions: What are the Types of Relations
Math?, What are the Different Types of Relation and Functions?
Related Quarries: relation of sets examples, types of relations, set theory relations, what is a relation in math, types of relation in math, how to find relation between two sets, what is relation in discrete mathematics.
Example Of Relation
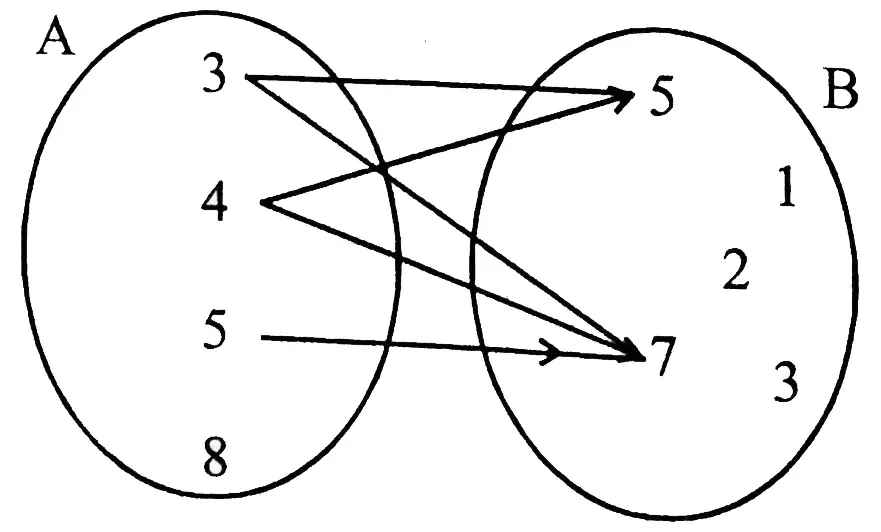
As an illustration,
let A = {3, 4, 5, 8} and B = {1, 2, 3, 5, 7}
Now let us associate those elements of A with the elements of B which satisfy the relation ’x is
less than y' where x Є A and y Є B.
In the Venn diagram we have shown the connections by arow marks. (3, 5)
is such an ordered pair where 3eA, 5 e B and 3<5.
Now all such ordered pairs constitute the relation R which is written as R = {(3, 5), (3, 7), (4, 5), (4, 7), (5, 7)}
Definition
The relation R from a non-empty set A to a non empty set B is a
subset of the cartesian product A x B.
Therefore, if R: A⟶B is a relation then R = {(a, b) | aRb,
a Є A, b Є B) is a subset of A x B.
Here 'nRb' stands for 'a is related to b'. It is also sometimes
denoted by a ⟶ b or (a, b) Є R. The elements of A which are related to the elements of B are
connected by 'arrow marks'. Such a diagram is called an 'arrow
diagram.
Representation Of Relation
Let S = {1, 2, 3, 4, 5} be a set. Let R: S⟶S be a relation such that
xRy if x<y where x, y Є S. Then this relation can be represented in the following different
ways
(1) Rule or set builder method
R ={(x, y) : xRy if x<y for x, y Є S. and S is the set of natural numbers less than 6}
(2) Roster or tabular method
R = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4),
(3, 5), (4, 5)}
(3) As a graph in the cartesian co-ordinate plane by plotting the
points (x, y) where xRy if x<y and x, y Є S. Here A, B, C, represent the respective ordered pairs
given in the tabular form of R.
Types Of Relation
There are four different types of relation in sets. Here we are
going to discuss all the types of relation one by one.
1. Inverse Relation: Let R be a relation from A to B. Then
another relation S from B to A is called the inverse of R if S
= {(b, a) : {a, b) Є R}. In this case S is denoted by 1/R or R^-1.
Example : Let A = {l, m, n} and B = {p, q, r}. Suppose R is a relation from A to B where R = {(l, q), (1,r), (m, p), (n, p), (n, r). Then the inverse relation of R from B to A is R^-1 = {(q, l), (r, l)}, (p, m), (p, n), (r n)}
Again we have seen that
d(R) = {l, m, n} and r(R) = {q, r p}
and
d(R^-1) = {q, g, p} and r(R ˡ) = {1, m, n}
∴ d(R) = r(R^-1) and d(R^-1) = r(R)
Note : It is to be noted that if R is any relation then
(l) it has always an inverse relation
(2) domain of R = range of R^-1, i.e. d(R) = r(R^-1)
(3) range of R = domain of R^-1, i.e. r(R) d(R^-1)
2. Identity Relation: Let A be a set. Then a relation on A is
called the identity relation if every element of A is related to itself.
In other words R:A⟶A1s called the identity relation if R= {(a, a} : for all a Є A}.
The identity relation is usually denoted by IA (where A is the set on which the relation is defined) or simply
by I. In the identity relation d(R) = r(R).
Example : Let A {a, b, c, d}. Then the identity relation on A
is I {a, a), {b, b), (fi, C)$ {d. d)}
Here d(I) = {a, b, c, d} and r(I) = {a, b, c, d}
Note : Rt us construct the matrix table of the identity relation of the
above example. The matrix table is as below-
|
|
a
|
b
|
c
|
d
|
|
a
|
1
|
0
|
0
|
0
|
|
b
|
0
|
1
|
0
|
0
|
|
c
|
0
|
0
|
1
|
0
|
|
d
|
0
|
0
|
0
|
1
|
It is noticed that all the entries dong the leading diagonal are 1 and the others are zero.
Tags:
Mathematics