7. A={3,6,8,9} is a set and aRb iff a-b is divisible by 3 for a,b Є A. Then (i) Write R as a set and draw the arrow diagram. (ii) Find d(R) and r(R). (iii) Can we find the inverse of R - Advance Math Class 10 - Exercise
1.3.
Related Quarries: range of relation example, let a = 2 3 4 5 6 let r be the relation on a defined by, let a = 1 2 3 4 6 let r be the relation on a defined by, let a= 1 2 3 4 5 6 define a relation r from a to a by r= (x y) y=x+1, identify the range of the relation, domain and range of a relation, domain and range of a relation examples, let a = 1 2 3 4 let r be the relation on a defined by
Solution:
Given,
A = {3, 6, 8, 9}
(i) Write R as a set and draw the arrow diagram
R = {aRb iff a-b is divisible by 3 ∀ a, b Є A}
∴R = {(3, 3), (3, 6), (3, 9), (6, 3), (6, 6), (6, 9), (9, 3), (9, 6), (9, 9)}
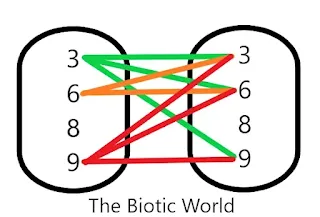
|
| Arrow Diagram |
(ii) Find d(R) and r(R)
d(R) = {3, 6, 9}
r(R) = {3, 6, 9}
(iii) Can we find the inverse of R
R^-1 = { (3, 3), (6, 3), (9, 3), (3, 6), (6, 6), (9, 6), (3, 9), (6, 9), (9, 9)}
⇒ R^-1= R, so we can't find the reverse of R.
Exercise: 1.3
1. If A = {1, 3}, then write the identity relation I : A⟶A. Also write the universal relation on A ?
2. If A = {1, 2} then write down all the relation on A ?
3. If A = (1, 2, 3) then find the elements of the relation R= {(x, y): x=y and x, y Є A} on A ?
6. Determine R^-1 of the relation R given in question 5 above. Also find d(R^-1) and r(R^-1) ?