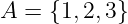3. If A = (1, 2, 3) then find the elements of the relation R= {(x, y): x=y and x, y Є A} on A.
Related Quarries: let a = (1, 2, 3, 4, 5, 6 define a relation r), a= 1 2 3 4 5 6 r= (x y) y is divisible by x, let a = (1, 2, 3,...,14 define a relation r from a to a), define a relation r on the set n of natural numbers by r= (x y) y=x+5, relation r in the set n of natural numbers defined as y=x+5, let a 1 2 3 4 5 6 define a relation r from a to a by r {( x y y x 1 then write the elements of r, let a 1 2 3 14 define a relation r from a to a by r= (x y) 3x-y=0, relation r in the set z of all integers defined as r= (x y) x-.
Here,
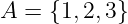
R= {(x, y): x=y and x, y Є A}
= {(1, 1), (2, 2), (3,3)}
Exercise: 1.3
1. If A = {1, 3}, then write the identity relation I : A⟶A. Also write
the universal relation on A ?
2. If A = {1, 2} then write down all the relation on A ?
3. If A = (1, 2, 3) then find the elements of the relation R= {(x, y):
x=y and x, y Є A} on A ?
4. Z + is the set of positive integers and R: Z+ → Z+ is a relation
defined as R = {(a, b) | a, b Є Z+ and a-b >2}. Is it a finite
relation? Represent R as a set in the Roster form ?
5. A={2,3,4,5} and B={3,6,7,10} be two sets and a relation R is defined
as R={(x, y): x completely divides y where x Є A and y Є B}. Write the
relation R in the tabular form. Also represent R by arrow diagram and
matrix table ?
6. Determine R^-1 of the relation R given in question 5 above. Also find
d(R^-1) and r(R^-1) ?
7. A={3,6,8,9} is a set and aRb iff a-b is divisible by 3 for a,b Є A.
Then (i) Write R as a set and draw the arrow diagram. (ii) Find d(R) and
r(R). (iii) Can we find the inverse of R ?
8. A={1,2,3,4} and B={a,b,c,d} be two sets. Choose which of the
followings are relation from A to B ?
9. A relation R is defined on the the set of natural N as aRb where a=b^2
for a,bЄN. Write the relation R. Also write R^-1 in set builder method
?
10. If A={1,2,3,4,6} and R is a relation on A defined as R={(x,y):y is
exactly divisible by x where x,yЄA} then ?
11. Let A = {10, 11, 12, 13} and B = {1, 2, 3, 4} be two sets. Write the
following relations from A to B as defined in each case ?
12. R1 and R2 be two relations on the set of integers Z defined as below
-(i) R1={(a,b):a^2=b^2 and a,b∈Z} (ii) R2={(a,b): a-b is positive where
a,b are primes and both are smaller than 10} determine the domain and the
range of each of them ?