Why factorial of zero is equals to one not zero - 0! = 1 ?

Factorial is a mathematical operator. If we take factorial of 5 then its equal to 5x4x3x2x1. Factorial is represented by ! or ㄴ. If n is the number then factorial of n can be represented by n! or ।n.

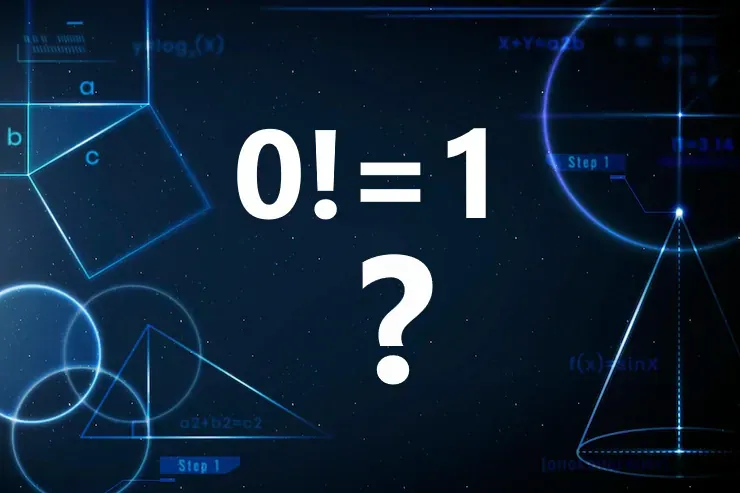Why factorial of zero is equals to one not zero - 0! = 1 ?

  Follow Us  

For example:

2! = 2x1

3! = 3x2x1

4! = 4x3x2x1

5! = 5x4x3x2x1

n! = nx(n-1)x(n-2)x(n-3)x.............

From above now we have a basic idea about factorial. We have a got a chapter called Permutation and Combination in class 10, 11 and 12 mathematics or advance mathematics.

From that chapter we know, When r ≤ n then

ⁿP_r=n! / (n-r)!

⇒Now when r = 1

⇒ⁿP₁=n! / (n-1)!
⇒ⁿP₁=n(n-1)! / (n-1)!
⇒ⁿP₁=n

⇒Now when r = 2

⇒ⁿP₂=n! / (n-2)!
⇒ⁿP₂=n(n-1)(n-2)! / (n-2)!
⇒ⁿP₂=nx(n-1)

⇒Now when r = 3

⇒ⁿP₃=n! / (n-3)!
⇒ⁿP₃=n(n-1)(n-2)(n-3)! / (n-3)!
⇒ⁿP₃=nx(n-1)x(n-2)

From above we can conclude that

ⁿP₁=n
ⁿP₂=nx(n-1)
ⁿP₃=nx(n-1)x(n-2)

ⁿP_n=nx(n-1)x(n-2)x(n-3)x........=n!

ⁿP_n=n!

⇒n! / (n-r)!=n!
⇒n! / (n-n)!=n!
⇒n! / 0!=n!
⇒0!=n! / n!

⇒0!=1

That is why factorial of zero is equal to one note zero i.e. 0! = 1 is true.